Как нам известно из закона Ома, ток на участке цепи находится в следующей зависимости: I=U/R. Закон был выведен в результате серии экспериментов немецким физиком Георгом Омом в XIX веке. Он заметил закономерность: сила тока на каком-либо участке цепи прямо зависит от напряжения, которое к этому участку приложено, и обратно - от его сопротивления.
Позже было установлено, что сопротивление участка зависит от его геометрических характеристик следующим образом: R=ρl/S,
где l- длина проводника, S - площадь его поперечного сечения, а ρ - некий коэффициент пропорциональности.
Таким образом, сопротивление определяется геометрией проводника, а также таким параметром, как удельное сопротивление (далее - у. с.) - так назвали этот коэффициент. Если взять два проводника с одинаковым сечением и длиной и поставить их в цепь по очереди, то, измеряя силу тока и сопротивление, можно увидеть, что в двух случаях эти показатели будут разными. Таким образом, удельное электрическое сопротивление - это характеристика материала, из которого сделан проводник, а если быть еще более точным, то вещества.
Проводимость и сопротивление
У.с. показывает способность вещества препятствовать прохождению тока. Но в физике есть и обратная величина — проводимость. Она показывает способность проводить электрический ток. Выглядит она так:
σ=1/ρ, где ρ - это и есть удельное сопротивление вещества.
Если говорить о проводимости, то она определяется характеристиками носителей зарядов в этом веществе. Так, в металлах есть свободные электроны. На внешней оболочке их не больше трех, и атому выгоднее их "отдать", что и происходит при химических реакциях с веществами из правой части таблицы Менделеева. В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.
В растворах носителями заряда являются ионы.
Если говорить о таких веществах, как кремний, то по своим свойствам он является полупроводником и работает несколько по иному принципу, но об этом позже. А пока разберемся, чем же отличаются такие классы веществ, как:
- Проводники;
- Полупроводники;
- Диэлектрики.
Проводники и диэлектрики
Есть вещества, которые ток почти не проводят. Они называются диэлектриками. Такие вещества способны поляризоваться в электрическом поле, то есть их молекулы могут поворачиваться в этом поле в зависимости от того, как распределены в них электроны. Но поскольку электроны эти не являются свободными, а служат для связи между атомами, ток они не проводят.
Проводимость диэлектриков почти нулевая, хотя идеальных среди них нет (это такая же абстракция, как абсолютно черное тело или идеальный газ).
Условной границей понятия «проводник» является ρ<10^-5 Ом, а нижний порог такового у диэлектрика - 10^8 Ом.
Между этими двумя классами существуют вещества, называемые полупроводниками. Но выделение их в отдельную группу веществ связано не столько с их промежуточным состоянием в линейке «проводимость - сопротивление», сколько с особенностями этой проводимости в различных условиях.
Зависимость от факторов внешней среды
Проводимость - не совсем постоянная величина. Данные в таблицах, откуда берут ρ для расчетов, существуют для нормальных условий среды, то есть для температуры 20 градусов. В реальности для работы цепи сложно подобрать такие идеальные условия; фактически у.с. (а стало быть, и проводимость) зависят от следующих факторов:
- температура;
- давление;
- наличие магнитных полей;
- свет;
- агрегатное состояние.
Разные вещества имеют свой график изменения этого параметра в разных условиях. Так, ферромагнетики (железо и никель) увеличивают его при совпадении направления тока с направлением силовых линий магнитного поля. Что касается температуры, то зависимость здесь почти линейная (существует даже понятие температурного коэффициента сопротивления, и это тоже табличная величина). Но направление этой зависимости различно: у металлов оно повышается с повышением температуры, а у редкоземельных элементов и растворов электролитов увеличивается - и это в пределах одного агрегатного состояния.
У полупроводников зависимость от температуры не линейная, а гиперболическая и обратная: при повышении температуры их проводимость увеличивается. Это качественно отличает проводники от полупроводников. Вот так выглядит зависимость ρ от температуры у проводников:
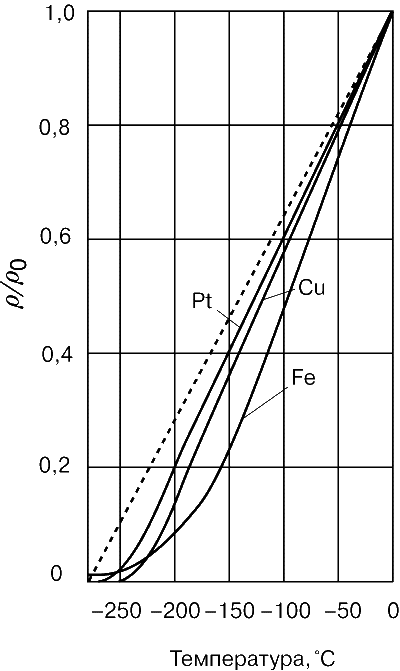
Здесь представлены удельное сопротивление меди, платины и железа. Немного другой график у некоторых металлов, например, ртути — при понижении температуры до 4 К она теряет его почти полностью (такое явление называется сверхпроводимостью).
А для полупроводников эта зависимость будет примерно такая:
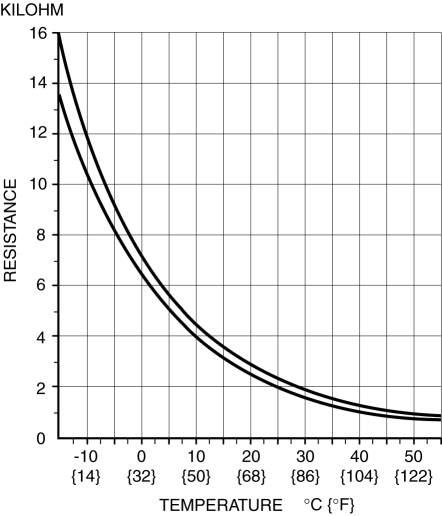
При переходе в жидкое состояние ρ металла увеличивается, а вот дальше все они ведут себя по-разному. Например, у расплавленного висмута оно ниже, чем при комнатной температуре, а у меди - в 10 раз выше нормального. Никель выходит из линейного графика еще при 400 градусах, после чего ρ падает.
Зато у вольфрама температурная зависимость настолько высока, что это становится причиной перегорания ламп накаливания. При включении ток нагревает спираль, и ее сопротивление увеличивается в несколько раз.
Также у. с. сплавов зависит от технологии их производства. Так, если мы имеем дело с простой механической смесью, то сопротивление такого вещества можно посчитать по среднему, а вот оно же у сплава замещения (это когда два и более элемента складываются в одну кристаллическую решетку) будет иным, как правило, куда большим. Например, нихром, из которого делают спирали для электроплиток, имеет такую цифру этого параметра, что этот проводник при включении в цепь греется до красноты (из-за чего, собственно, и используется).
Вот характеристика ρ углеродистых сталей:
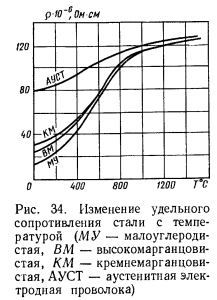
Как видно, при приближении к температуре плавления оно стабилизируется.
Удельное сопротивление различных проводников
Как бы то ни было, а при расчетах используется ρ именно в нормальных условиях. Приведем таблицу, по которой можно сравнить эту характеристику у разных металлов:
| металл | удельное сопротивление, Ом·м | температурный коэффициент, 1/°С* 10^-3 |
| медь | 1,68*10^-8 | 3,9 |
| алюминий | 2,82*10^-8 | 3,9 |
| железо | 1*10^-7 | 5 |
| серебро | 1,59*10^-8 | 3,8 |
| золото | 2,44*10^-8 | 3,4 |
| магний | 4,4*10^-8 | 3,9 |
| олово | 1,09*10^-7 | 4,5 |
| свинец | 2,2*10^-7 | 3,9 |
| цинк | 5,9*10^-8 | 3,7 |
Как видно из таблицы, лучший проводник - это серебро. И только его стоимость мешает массово применять его в производстве кабеля. У.с. алюминия тоже небольшое, но меньше, чем у золота. Из таблицы становится понятно, почему проводка в домах либо медная, либо алюминиевая.
В таблицу не включен никель, у которого, как мы уже сказали, немного необычный график зависимости у. с. от температуры. Удельное сопротивление никеля после повышения температуры до 400 градусов начинает не расти, а падать. Интересно он ведет себя и в других сплавах замещения. Вот так ведет себя сплав меди и никеля в зависимости от процентного соотношения того и другого:
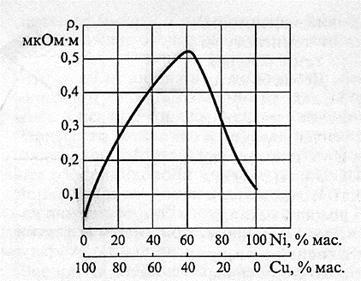
А этот интересный график показывает сопротивление сплавов Цинк - магний:
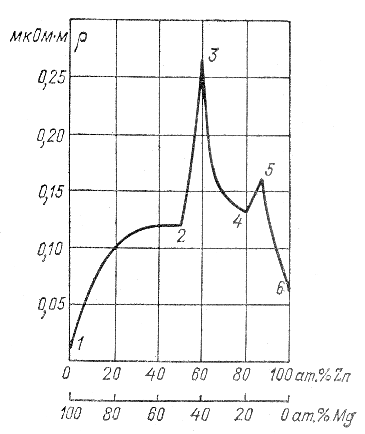
В качестве материалов для изготовления реостатов используют высокоомные сплавы, вот их характеристики:
| сплав | удельное сопротивление |
| манганин | 4,82*10^-7 |
| константан | 4,9*10^-7 |
| нихром | 1,1*10^-6 |
| фехраль | 1,2*10^-6 |
| хромаль | 1,2*10^-6 |
Это сложные сплавы, состоящие из железа, алюминия, хрома, марганца, никеля.
Что касается углеродистых сталей, то оно составляет примерно 1,7*10^-7 Ом · м.
Разница между у. с. различных проводников определяет и их применение. Так, медь и алюминий массово применяются при производстве кабеля, а золото и серебро - в качестве контактов в ряде радиотехнических изделий. Высокоомные проводники нашли свое место среди производителей электроприборов (точнее, они и создавались для этого).
Изменчивость этого параметра в зависимости от условий внешней среды легла в основу таких приборов, как датчики магнитного поля, терморезисторы, тензодатчики, фоторезисторы.
